如何以Arduino使用ADS1115 ADC的連續模式

德州儀器ADS1115是一個16位元的類比數位轉換器(ADC)。這個ADC是基於ΔΣ架構，取樣率最高為860Hz。 ADS1115必須操作在連續模式(Continuous Mode)下才可以用最高860Hz的取樣率來做轉換。 在這篇文章中，我們會示範如何在Arduino環境下設定ADS1115使用連續模式，並且以860Hz取樣率做轉換。

Raspberry Pi Pico - 如何一次設定多個GPIO (Mask Set)

在Raspberry Pi Pico程式中，我們通常會使用gpio_set()來設定一個腳位的數值。 像是在簡單的Blink程式中，我們會這樣寫：

    while(true) {
        gpio_set(led_pin, 1);
        sleep_ms(1000);
        gpio_set(led_pin, 0);
        sleep_ms(1000);
    }

如果我們要一次設定更多隻腳的話，直覺上我們可能會寫更多行的gpio_set()。

    gpio_set(pin1, value1);
    gpio_set(pin2, value2);
    // ...
    gpio_set(pinN, valueN);

這樣子如果要設定N隻腳的話，就要寫N行程式，有點沒效率。 其實有更聰明的方法可以只用一行就達到一樣的目的，這個方法叫做mask set。 在實作之前，我們需要了解一下GPIO的數值(0和1)是怎麼被設定的。

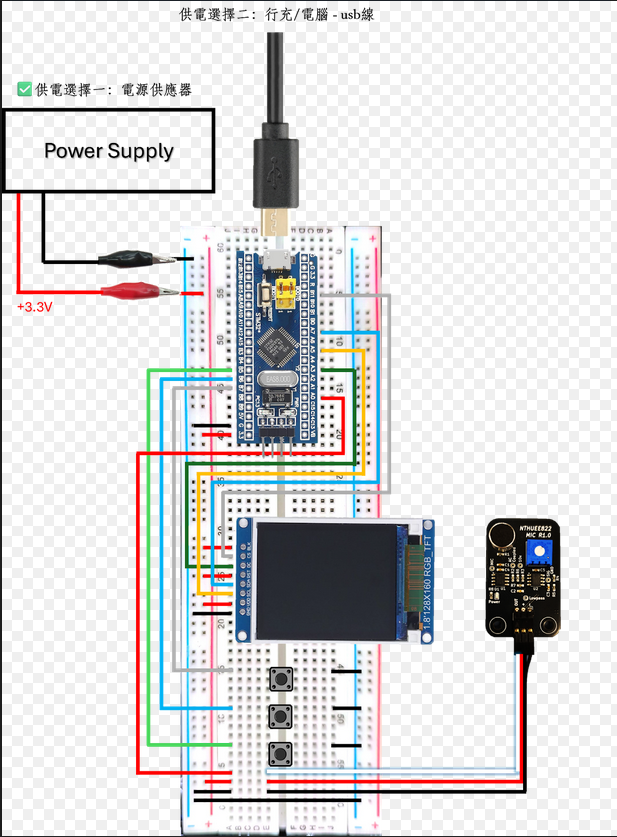
2026清大電機體驗營

目錄

• 傅立葉分析簡介
• SPI通訊協議
• Flappy Bird 程式介紹
• 基礎電路學
• 麥克風模組詳細原理
• 組裝詳細步驟

傅立葉分析

傅立葉分析(Fourier Analysis)是電機工程領域中最重要的數學方法之一，它讓我們可以從頻率的角度來看世界。傅立葉分析的精神就是所有的訊號都可以拆成無限多個正弦(sine)波和餘弦(cosine)波的疊加，就像空間座標可以拆成(x, y, z)分量。任何週期性的訊號都可以寫成以下形式。假設週期為T，我們會定義基礎頻率(fundamental frequency, $\omega_0 = \frac{2\pi}{T}$)。

$$ f(x) = a_0 + \sum_{n=1}^\infty [a_n \cos(n\omega_0 t) + b_n \sin(n\omega_0 t)] $$

其中，係數$a_n$和$b_n$代表n倍基礎頻率($n_0$)的餘弦波和正弦波的強度。我們可以將他們對頻率作圖得到頻譜(spectrum)，就像五線譜一樣顯示什麼頻率有訊號，什麼頻率沒有。那麼我們要怎麼找到$a_n$和$b_n$這些係數呢？答案是用向量內積(inner product)。對兩個週期性訊號做內積就是兩個訊號相乘取一個週期的平均。

$$ a_n = \frac{2}{T} \int_{0}^{T} f(t)cos(n\omega_0t) dx $$