2026清大電機體驗營
目錄
傅立葉分析
傅立葉分析(Fourier Analysis)是電機工程領域中最重要的數學方法之一,它讓我們可以從頻率的角度來看世界。傅立葉分析的精神就是所有的訊號都可以拆成無限多個正弦(sine)波和餘弦(cosine)波的疊加,就像空間座標可以拆成(x, y, z)分量。任何週期性的訊號都可以寫成以下形式。假設週期為T,我們會定義基礎頻率(fundamental frequency, $\omega_0 = \frac{2\pi}{T}$)。
$$ f(x) = a_0 + \sum_{n=1}^\infty [a_n \cos(n\omega_0 t) + b_n \sin(n\omega_0 t)] $$
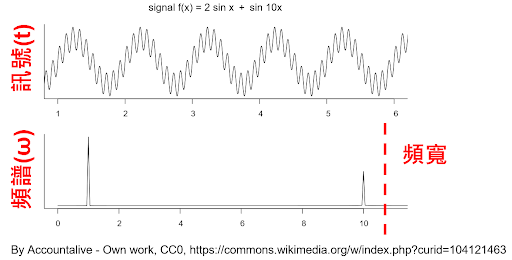
其中,係數$a_n$和$b_n$代表n倍基礎頻率($n_0$)的餘弦波和正弦波的強度。我們可以將他們對頻率作圖得到頻譜(spectrum),就像五線譜一樣顯示什麼頻率有訊號,什麼頻率沒有。那麼我們要怎麼找到$a_n$和$b_n$這些係數呢?答案是用向量內積(inner product)。對兩個週期性訊號做內積就是兩個訊號相乘取一個週期的平均。
$$ a_n = \frac{2}{T} \int_{0}^{T} f(t)cos(n\omega_0t) dx $$
那我們n要算到第幾個呢?只要算到訊號的頻寬(bandwidth)就好了。自然界的系統都有速度限制,例如:電線中的訊號無法無限快、人耳的耳蝸無法震動太高頻。這個最高可用頻率就叫頻寬。
取樣與量化
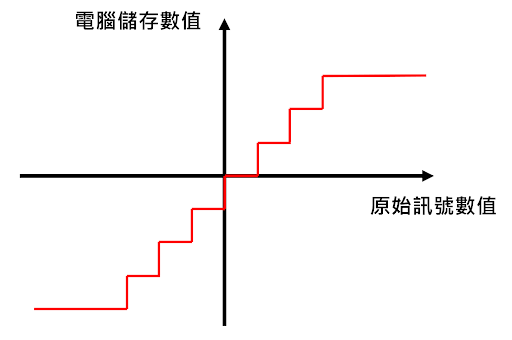
我們是工程師,所以除了理論上傅立葉怎麼算,我們更在乎實際上要怎麼用電腦算出來。在電腦的世界中,時間和數字都是一格一格(discrete)的。首先,電腦是利用位元(bit)來儲存資料。位元是電腦中最小的資料單位,一個位元的數值只可以是0或1。電腦中的位元數量有限,所以只能存下有限多種數值。因此,電腦能儲存的兩個數字之間會有一段無法儲存的數值,而必須四捨五入,這個動作稱作量化(quantization),並且會造成量化誤差。
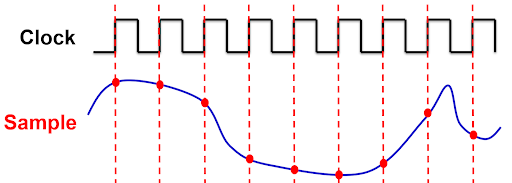
電腦的運作是依照一個稱為時脈(clock)的訊號,電腦中所有的運算都在時脈由低變高的那一瞬間執行。因此,電腦只能看到這些瞬間的訊號的數值。這個動作稱為取樣(sampling)。
經過取樣和量化之後,就可以把資料存在電腦的記憶體裡面做計算了。電腦針對取樣過後的訊號做的傅立葉分析稱為離散傅立葉變換(DFT)。科學家(Cooley和Tukey)透過改變運算的順序,使得電腦算傅立葉分析變得更快,成為現今常用的快速傅立葉變換(FFT)演算法。
Nyquist取樣定理
取樣和量化會造成資料精確度的流失。量化誤差就像尺的最小刻度,我們只要使用更多位元就可以降低量化誤差。可是取樣造成的效應就比較玄一點。先說結論,科學家Nyquist推導出來只要取樣頻率(sampling frequency)比訊號的頻寬大兩倍以上,就可以完整地代表原本在連續時間中的訊號。
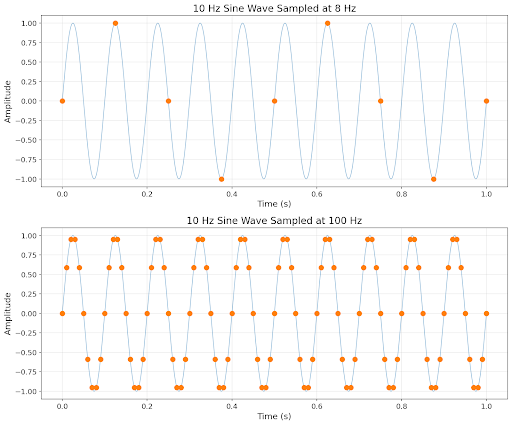
如果我們的取樣頻率太慢,就會出現混疊(aliasing)的效應。從取樣出來的數據點還原出來的訊號除了流失掉高頻的部分,還會出現原本不存在的頻率。
Serial Communication-SPI
我們無法拉上萬條線連接螢幕和電腦,所以我們須要在時間上切割這些資料。例如,一筆 1024 bit 的資料分成 4 份傳送,只需要 256 條線。如果把這件事作到極致,只用 1 條線傳送資料,就是串列通訊(serial communication)。 如果資料量很大,這條線上的電壓需要以非常高的頻率在0和1之間切換。一樣用上面的一張圖片 60kB 來算,如果每秒要有 24 禎,這條資料線要可以每秒變化 140 萬次(1.44 MHz)。雖然聽起來很快,但其實對現代電腦來說是一項輕鬆的工作。 除此之外,電腦和螢幕之間要講好用哪種語言溝通,這個大家說好的語言我們稱之為協議(protocol)。協議會規定需要幾條線、每條線的作用,以及每條線在時間上如何變化。
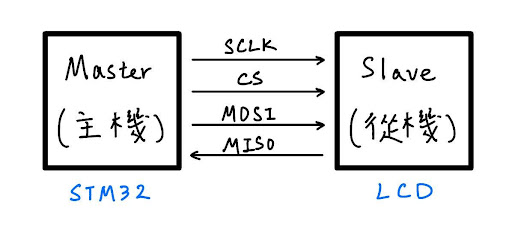
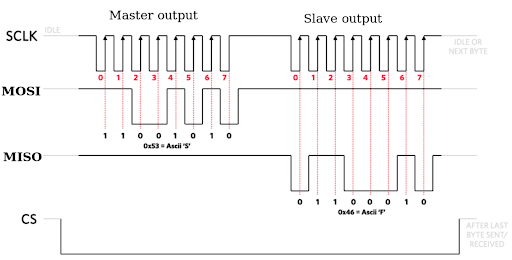
這個 project 的螢幕用的協議是 SPI(Serial Peripheral Interface),一共有四條訊號線:用於同步的時脈訊號(clock, SCLK),選擇是否啟用裝置的 chip select(CS),以及用來輸出、輸入資料的 MOSI (master out slave in), MISO (master in slave out)。Master負責下指令,控制 SCLK、CS 和 MOSI。Slave接收這三個訊號,並且透過 MISO 回覆 Master。Slave 收到 CS = 0 時才會工作,而資料的傳遞只會發生在 SCLK 改變的那瞬間,我們稱為邊緣觸發(edge triggered)。舉例來說,如果今天大家講好是 SCLK 從 0 變成 1 的那瞬間傳資料,這叫正緣觸發(rising edge triggered),此時 master 藉由 MOSI 輸出資料給 slave,同時藉由 MISO 接收 slave 傳來的資料。
| 訊號線 | SCLK | CS | MOSI | MISO |
|---|---|---|---|---|
| 功能 | 資料同步 | 選擇是否啟用該slave | master 傳給 slave | slave 傳給 master |
下圖是一次 SPI 傳輸期間四條訊號線的變化。首先,Master 會將 CS 由1變成0,通知 slave 要開始傳資料了。接下來,SCLK會開始變化,同時 MOSI 會把要傳的資料送出去。當 slave收到資料後,會依照指令透過 MISO 回應 master。
🎮 Flappy Bird 聲控遊戲使用說明
🔘 按鍵功能總覽
| 顏色 | 按鍵 | 功能 |
|---|---|---|
| 🟢 綠線(B5) | btn1 | 開始遊戲 / 暫停遊戲 / 進入選單 |
| 🔵 藍線(B6) | btn-rst | 重置最高分 |
| ⚪ 灰線(B7) | btn2 | 難度調整 / 結束遊戲 |

🏠 Step 1 — 進入選單畫面
開機後會看到首頁畫面,
按下 btn1 可進入選單。
⚙️ Step 2 — 選單功能與頻率偵測
在選單畫面中:
- 按 btn2 → 調整遊戲難度
- 按 btn1 → 開始遊戲
- 畫面會即時顯示麥克風偵測到的頻率
🎤 麥克風信號顏色說明
| 顏色 | 意義 |
|---|---|
| ⚪ 灰色 | 沒收到信號 / 訊號太弱 → 調整可變電阻 |
| 🟢 綠色 | 訊號正常 |
| 🔴 紅色 | 訊號過強 → 需調整麥克風可變電阻 |
🎮 Step 3 — 遊戲進行中
進入遊戲後:
- 透過 麥克風頻率 控制管子高度
- 按 btn1 → 暫停遊戲
- 按 btn2 → 立即結束遊戲
📡 聲音控制機制
管子高度會依照接收到的聲音頻率即時變化:
- 🎵 接收範圍:200 Hz ~ 600 Hz
- 📈 頻率越高 → 管子位置越高
- 📉 頻率越低 → 管子位置越低
電路
電路學簡介:
-
Kirchhoff's Circuit Laws - 克希荷夫電路定律
- Kirchhoff’s Current Law (簡稱:KCL)
→在電路上的每個節點,流入該點的電流總和=流出該點的電流總和
→備註:節點為電路中多條線接在一起的點
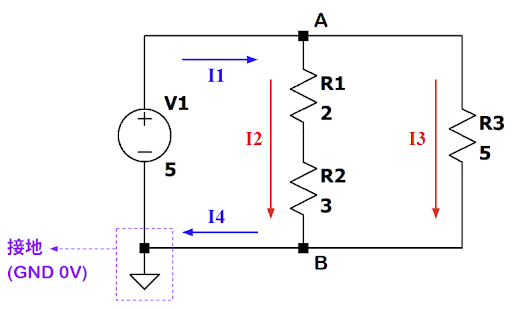
→對於A點:$I_1 (流入A點) = I_2+I_3 (流出A點)$
→對於B點:$I4 (流出B點) = I2+I3 (流入B點)$- Kirchhoff's Voltage Law (簡稱:KVL)
→環繞電路中任一迴圈的電位差總和為0
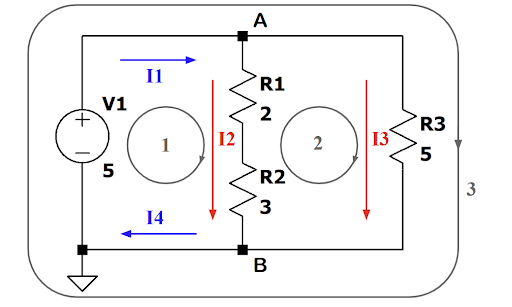
→上方電路總共有3個迴圈。若電流與迴圈方向相同則減去IR; 反之,若電流與迴圈方向相反則加上IR
→對於迴圈1:$5-R_1 \times I_2-R_2 \times I_2 = 0 \Rightarrow 5-2 \times I_2-3 \times I_2 = 0, I_2 = 1(A)$
→對於迴圈2:$0+R_2 \times I_2+R_1 \times I_2-R_3 \times I_3 = 0 \Rightarrow 5-5 \times I_3 = 0, I_3 = 1(A)$
→對於迴圈3:$5-R_3 \times I_3 = 0 \Rightarrow 5-5 \times I_3 = 0, I_3 = 1(A)$
→備註:計算時,電流方向可以先自行假設,若電流最終計算結果為負數,
則表示實際電流方向與最初假設的方向相反。- 例題:
請使用KCL計算出A點的電壓。
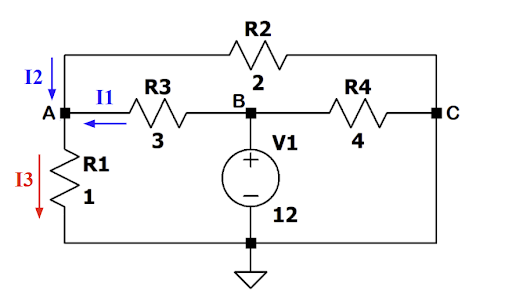
在A點使用KCL分析可知:$I_1+I_2=I_3$,又因為題目已定義C點為0V,故可知B點為12V,利用歐姆定律 $I= \frac{V}{R} $ 及已知值代入可得:$ \frac{12-A}{3}+ \frac{0-A}{2}= \frac{A-0}{1} \Rightarrow A= \frac{24}{11} \approx 2.18(V)$ 即可得知A點電壓。
- Kirchhoff’s Current Law (簡稱:KCL)
運算放大器 (op amp):
-
認識運算放大器
- 運算放大器(Operational Amplifier)簡稱op amp
- 電路符號
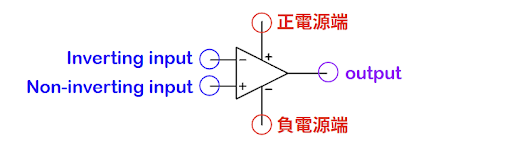
- 輸入及輸出關係 以下圖為例,兩端輸入分別接V1及V2、正電源端接5V、負電源端接0V
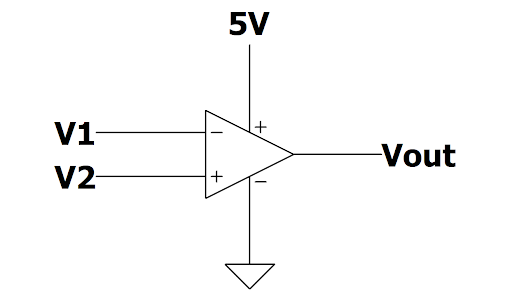
→Vout=A(V2-V1),其中A代表此op amp的增益(gain)
→增益(gain)可以想像成電路的放大能力,通常為某個倍數,如:10、100等
→Vout大小會被正負電源端(power supply)限制,如上圖 $0V \le V_{out} \le 5V$- 實際運用的考量
由於Vout=A(V2-V1),但大部分op amp的增益都非常大,若此時輸入有雜訊,將一同放大至Vout,則訊號會被干擾無法判定,因此我們通常不會直接使用訊號放大的功能,此時我們使用”回授(feedback)”以精準控制輸出及輸入的放大倍率,於下個段落詳細說明。
→備註:若output接回任意一個input則稱為回授(feedback)
-
運算放大器的應用
-
理想的op amp有以下三種特性
→輸入端沒有電流流入
→增益(gain)趨近於無限大
→當電路接為負回授,兩輸入端電壓幾乎相等,我們稱之為虛擬短路 -
負回授 (negative feedback) vs 正回授 (positive feedback)
→輸出(output)接回inverting input則為負回授,通常為虛擬短路
→輸出(output)接回non-inverting input則為正回授,通常沒有虛擬短路
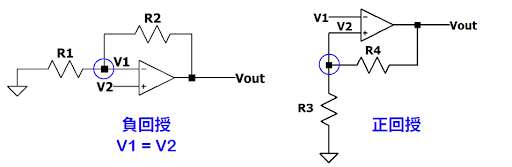
- Inverting amplifier
例圖:
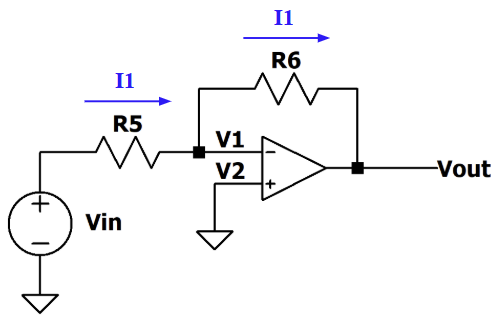
輸入輸出關係式推導: Vout經過 $R_6$ 接到inverting input,滿足前面負回授的條件,因此這個電路有虛擬短路(V1=V2),又因為理想op amp輸入端沒有電流流入,因此流經 $R_5$ 及 $R_6$ 的電流相同,故得到下方關係式: $$V1=V2=0, \; I_1= \frac{Vin-V1}{R5}= \frac{V1-Vout}{R6}$$ 解聯立後得到 $ V_{in}, V_{out}$的關係 $ \Rightarrow \frac{V_{out}}{V_{in}}=- \frac{R_6}{R_5}$
因為Vin和Vout為負數倍的關係,若Vin為sin波,則Vout則會上下顛倒並乘以 $ \frac{R_6}{R_5}$ 倍,故我們稱之為inverting amplifier。- Non-inverting amplifier
例圖:
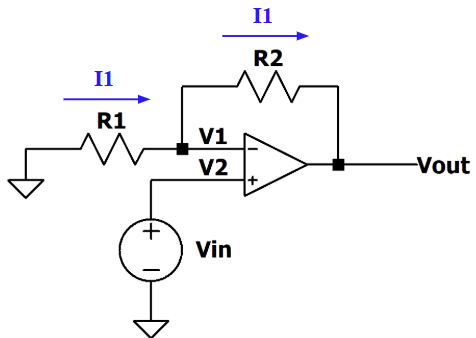
輸入輸出關係式推導:
$V_{out}$經過R2接到inverting input,滿足負回授且有虛擬短路(V1=V2),又因為理想op amp輸入端沒有電流流入,因此流經R1及R2的電流相同,故得到下方關係式: $$V1=V2=Vin, \quad I1= \frac{0-V1}{R_1}= \frac{V1-V_{out}}{R_2}$$ 解聯立後得到 $V_{in}, V_{out}$的關係 $ \frac{V_{out}}{V_{in}}=1+ \frac{R_2}{R_1}$ 由於 $V_{out}$ 為 $V_{in}$ 的正數倍,若 $V_{in}$ 為sin波,則 $V_{out}$ 則會放大 $1+ \frac{R_2}{R_1}$ 倍,形狀維持sin波,故我們稱之為Non-inverting amplifier。 -
Low Pass Filter:
- Bode Plot (波德圖)
描述系統在不同頻率下的變化,包含 gain 與 phase
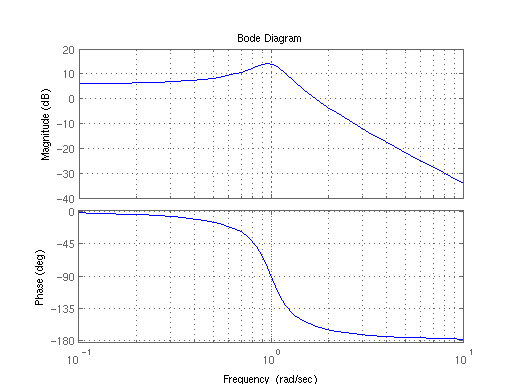
二階系統的波德圖 ( 擷取自維基百科
)
-
Gain / Magnitude (增益)
輸出訊號相對輸入訊號的比值,常用分貝 (dB) 表示:
$$Gain (dB) = 20 log | \frac{V_{out}}{V_{in}}|$$ 特性:
等於 0 → 輸出等於輸入、大於 0 → 輸出比輸入大、 小於 0 → 輸出比輸入小 -
Phase (相位)
輸出訊號相對輸入訊號的相位差,使用角度 (°) 表示
- 例子:
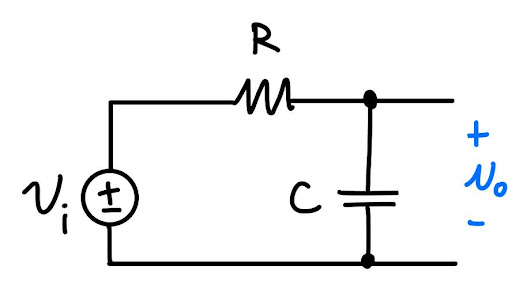
利用KCL,得知
$$ \frac{V_{out}}{Zc} = \frac{Vin}{R+Zc} \Rightarrow V_{out} = \frac{Zc}{R+Zc} Vin ( Zc = \frac{1}{j \omega C} )$$
$$\Rightarrow Gain = \frac{V_{out}}{V_{in}}= \frac{1}{1+j \omega CR}$$
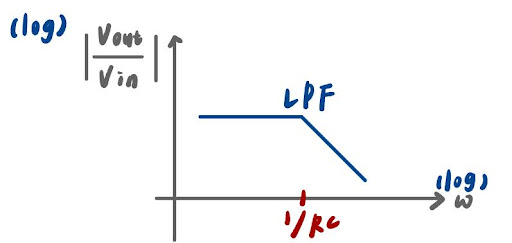
$$ \Rightarrow 取 1RC 為基準,$$
$$ \omega \ll /frac{1}{RC} ,gain = 1;$$
$$ \omega \gg \frac{1}{RC} ,gain = | \frac{1}{j \omega RC}|,取實數部分,可得 |\frac{1}{\omega RC}|$$
$$ \Rightarrow log| \frac{1}{ \omega RC}|=-log \omega -log RC$$
麥克風模組電路 deep dive
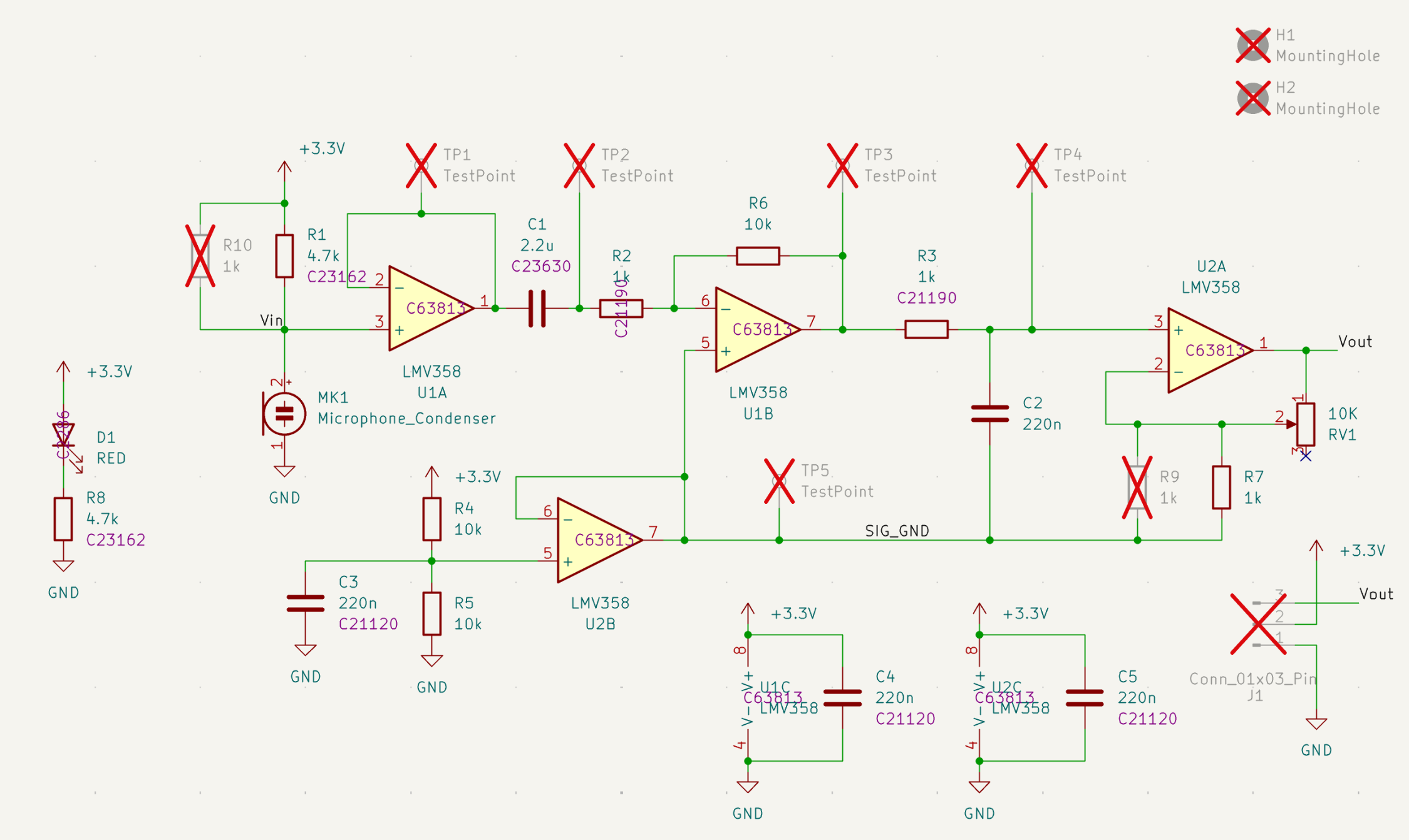
麥克風輸入
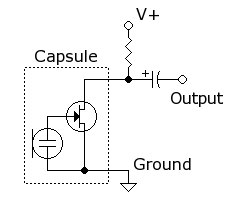
我們使用的麥克風是駐極式麥克風(electret microphone)。 在接收到聲音振動的時候,它內部會產生電壓的變化,並且透過一個場效應電晶體(field effect transistor)放大成為其輸出。
上圖是駐極式麥克風的示意電路圖,我們還需要在它的上方加一顆電阻,提供輸出電晶體所需要的偏壓電流(bias current)。 為了訊號的完整性,我們在麥克風的輸出用一顆運算放大器(operational amplifier或op-amp)做了一個電壓緩衝器(voltage buffer),如下圖所示。 在沒有聲音輸入的時候,偏壓電流和電阻會共同產生出一個直流電壓。 這一個電壓可能和後續放大器所需要的直流電壓不同,所以我們會再加上一顆電容來去除直流電壓差,只讓交流訊號通過。
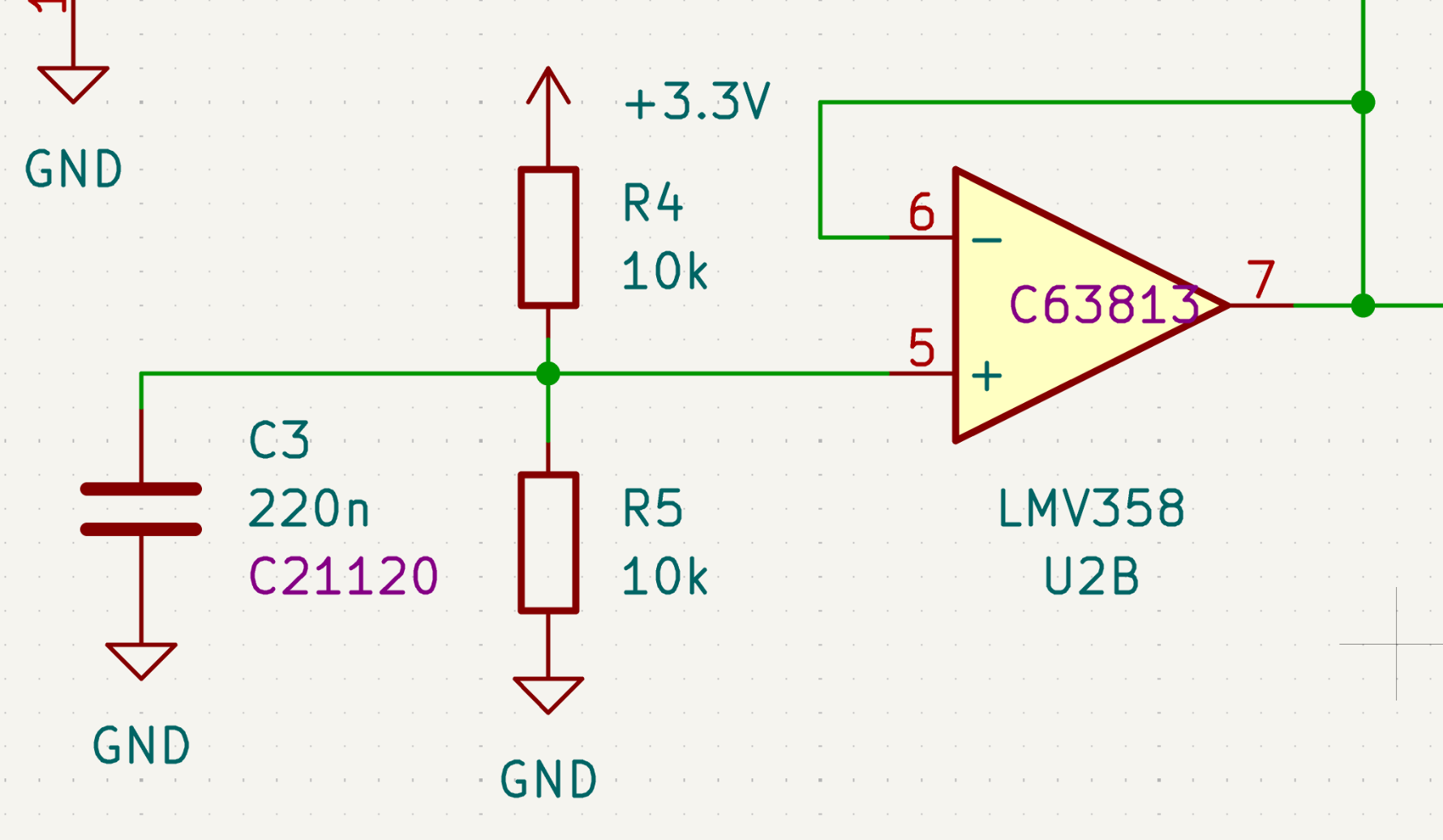
訊號參考電位(signal ground)
我們的麥克風模組是採用3.3V供電,最低電位為0V,最高電位為3.3V。 因為電路元件的限制,所有的訊號都只能在這個範圍中。 可是聲音的波形有正有負要怎麼辦? 我們須要把麥克風產生出來的波形平移使得它的平衡點在這個範圍的正中間,也就是1.65V。
為了讓電路可以做到這件事,我們必須先產生一個穩定的1.65V。 我們先用一個1:1的電阻分壓,從3.3V供電得到目標的1.65V。 但是,如果有電流流入或流出1.65V的點,這個電壓會受到嚴重的擾動。 因此,我們再用一個op-amp組成的voltage buffer來讓這個點有承受電流流入或流出的能力,使電壓穩定。
這個1.65V是我們所有訊號的參考電位,如果今天有一個訊號的實際電壓是2.4V,那麼它的訊號數值其實是2.4 - 1.65 = 0.75V。
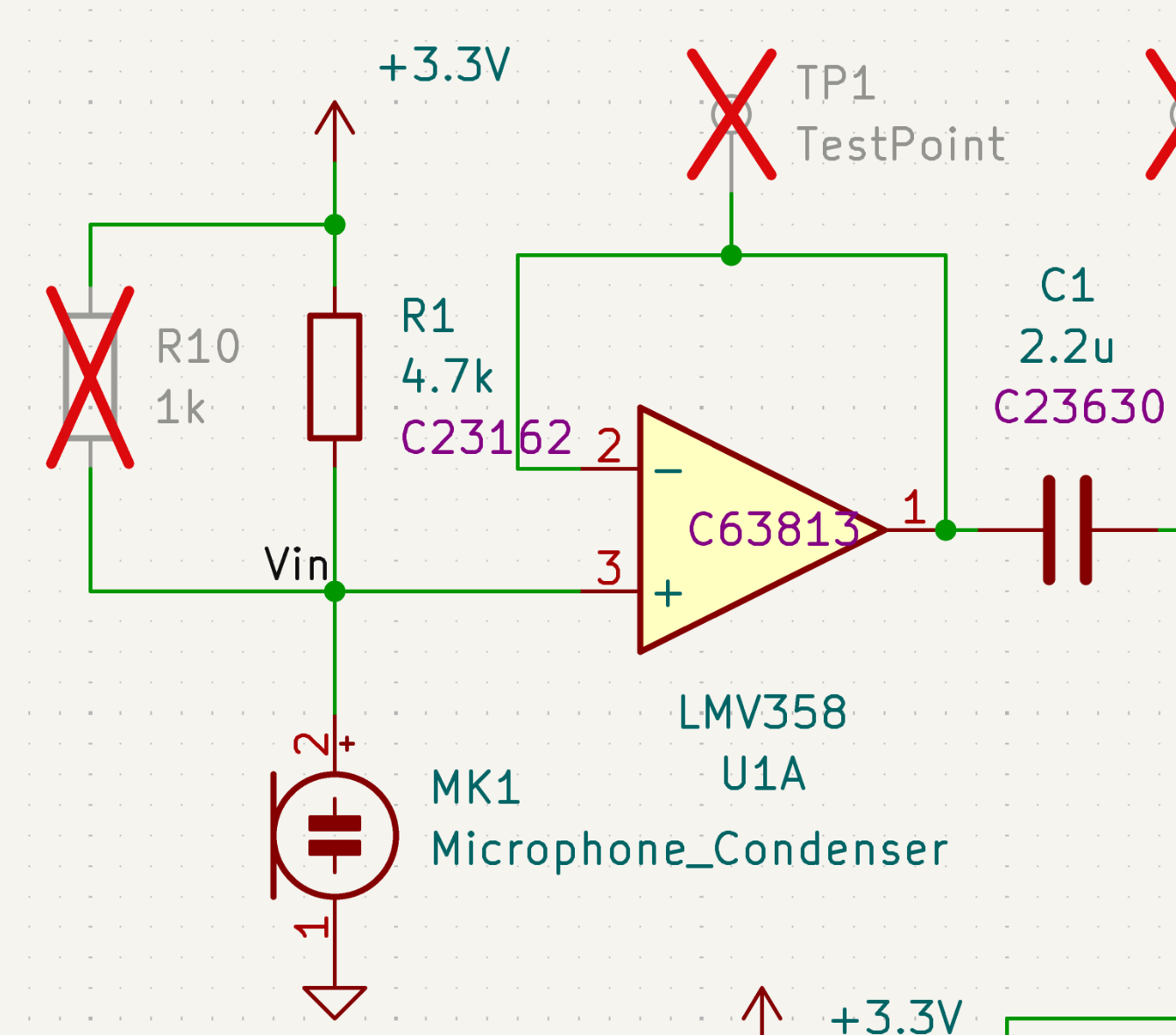
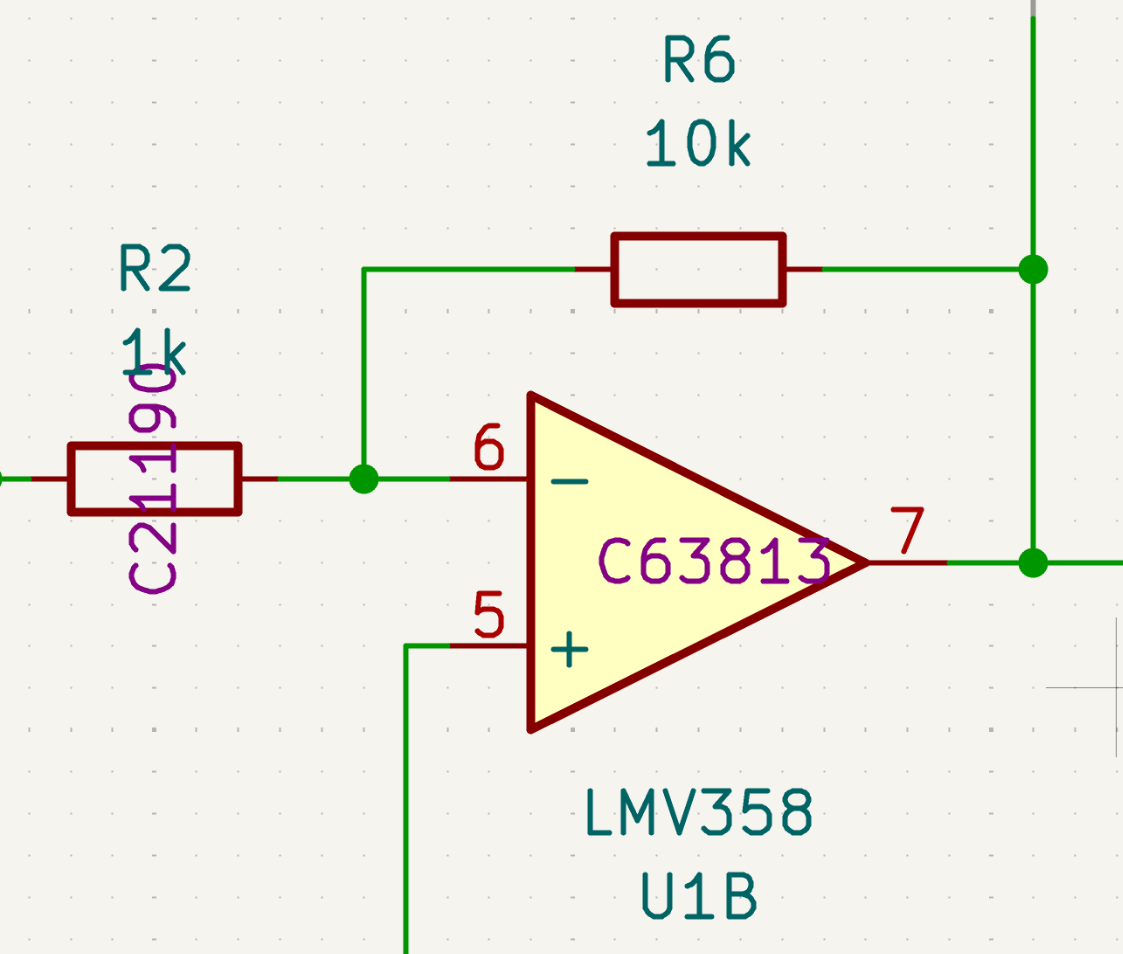
前級放大器(pre-amp)
因為麥克風輸出的訊號振幅很小,所以我們設計了一個增益(gain)10倍的放大器來放大訊號。 我們採用反向放大器的電路,除了振幅會放大10倍之外,還會把訊號的數值變成負的。 舉例來說,麥克風給出來的訊號假如是+0.1V的話,經過這個放大器得到的輸出會是-1.0V。 注意這邊的電壓都是相對1.65V的參考電位,所以實際上的電壓分別是1.75V和0.65V。
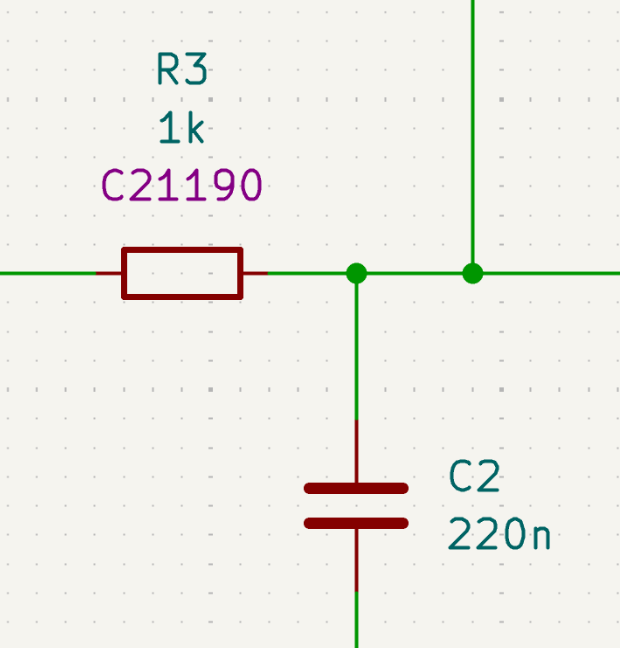
低通濾波器(low-pass filter)
為了降低麥克風的高頻雜訊以及後續取樣時高頻訊號造成的混疊(aliasing),我們必須降低高頻訊號的強度。 我們利用一個簡單的電阻電容低通濾波器,把-3dB截止頻率設定在723Hz。 在這個頻率之上,訊號振幅會和頻率呈反比衰減,也就是說到10000Hz以上的訊號會被壓制到原本的0.1倍以下。
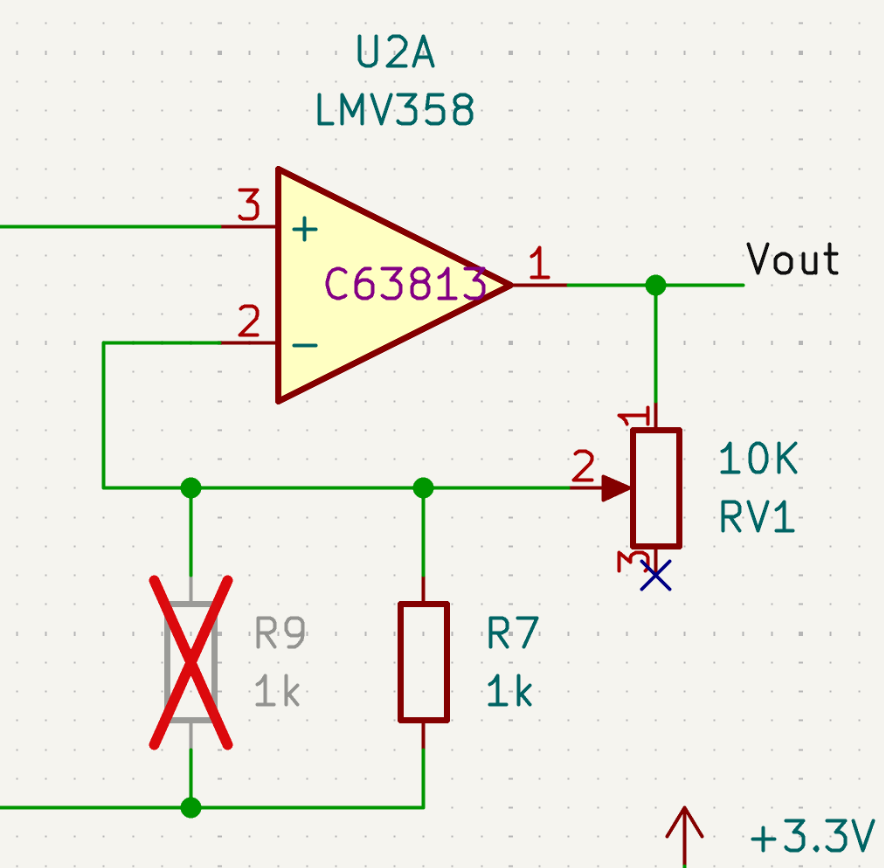
可調放大器
我們設計了第二級的放大器,並且讓它的gain是可調的。 這個放大器採用非反向的架構,因此不會把訊號的數值變成負的。 放大器的gain是由電阻R7和可變電阻RV1的分壓所決定,可調的範圍從2倍到11倍。